从 toFixed() 看「四舍五入法」的正确性

前言

「四舍五入」这条规则是每个人从小学就学到的一条小数舍入规则，无非是看舍去位是小于等于 4 还是大于等于 5。

那时候的我觉得它好像是公平的。

「0、1、2、3、4」一组，「5、6、7、8、9」一组，每组五个，谁也不欠谁。

但是，我的心里又总觉得哪里有些不对，苦于说不出来最后只好作罢。

但长大后，当我使用到 JavaScript 的 toFixed() 函数时，却惊讶地发现：它并不是一直都会四舍五入的。

(1.35).toFixed(1); // 1.4
(1.45).toFixed(1); // 1.4

为什么对于相同的尾数 5 的舍入，结果却不同呢？

我简单查阅了一下资料，有些人这么解释道：toFixed() 使用的是「银行家舍入法」。

银行家舍入法

什么是「银行家舍入法」呢？

银行家舍入法是由 IEEE 754 标准规定的浮点数取整算法，大部分的编程软件都使用这种方法。

该方法又被称为「四舍六入五取偶法」或者「四舍六入五留双法」。其规则是：

当舍去位的数值：

• 小于等于 4，直接舍去该位
• 大于等于 6，向前位进一

• 等于 5

  • 5 后有数，向前位进一

  • 5 后全 0

    • 5 前位数值为奇，则向前位进一（将前位凑成偶）
    • 5 前位数值为偶，则直接舍去该位

为什么会有这样的规则呢？如果银行家舍入法是对的，那我们一直以来十分信任的四舍五入岂不就错了？

我们先了解一下，为什么叫做银行家舍入法：

假如我们使用四舍五入法，且假设银行收到的钱中，要舍入的那位数在 0~9 是等概率的，那么假设银行分别收到了0.0, 0.1, ..., 0.9元，然后通过四舍五入法，银行能够得到五个0.0和五个1.0。

但是实际上，银行收到的总共的钱0.0 + 0.1 + ... + 0.9 = 4.5元，而银行日后却得为客户付还1.0 * 5 = 5.0元，这样银行就亏了0.5元钱了。

啊这到底是怎么回事，为什么看起来公平的事情，结果又变得并不公平？

有人可能发现了：在「舍去阵营」中，0.0其实并没有任何的损失，而「进位阵营」则或多或少都有好好地赚一笔。

那这样的话，我们不如不再考虑舍入位为 0 的情况，只取舍入位为 1 到 9 的情况，那么中位数就是 5 了，小于 5 的 1234 舍弃、大于 5 的进位……

等会，那 5 该怎么办？

于是银行家们又想到，要舍入的位置的前一位的数是奇是偶的情况是等概率的。

那么我们可以规定：

• 舍去位为 5，且其前位数值为奇，则向前位进一
• 舍去位为 5，且其前位数值为偶，则直接舍去该位

那么，这样就完美了么？

其实不然。银行家舍入法规定：当 5 作为舍入位时，舍入位后全为零时才根据其前位分奇偶舍入。否则直接进位。

为什么呢？其实也很好理解：

• 如果舍入位为小数的最后一位（也就是舍入位后全为零），那被舍入的尾数是离散的、可枚举的 0, 1, 2, ..., 9，1, 2, 3, 4 和 6, 7, 8, 9 分别一组，5 看情况对半分；
• 如果舍入位不是小数的最后一位，此时被舍入的尾数是连续的、不可枚举的，此时 0.5000... 才是这个舍入区间的中位数，0.499... 与 0.500...1 是对称的。

四舍五入的「正确性」

如果你已经认可了银行家舍入法的正确性，那你不可避免地要对四舍五入法产生了怀疑三连：四舍五入法错了吗？它又错在哪呢？为什么大家都用它？

我们回过来看看「四舍五入法」。

实际上，如果考虑无穷多位小数，那 0.5 整其实只是 (0.000..., 0.999...) 这个区间一个很小的点，从概率而言是约等于 0 的，所以在这种情况下，四舍五入确实做到了「五五开」。

但问题就是，我们遇到的小数一般都是有穷小数，如果我们只约去小数的最后一位，那么确实就出现了 0.1, 0.2, 0.3, 0.4 与 0.5, 0.6, 0.7, 0.8, 0.9 不对等的情况。

这就造成了在数学上，我们的「四舍五入法」是理论正确的；但在实际生活中（如以上的银行存钱问题），基本上都是有穷小数。无穷小数的「缺少」导致了四舍五入法不再严格正确。

那话就说回来了，为什么我们还在使用四舍五入法呢？

答案其实是很简单的，只有两个字——方便。

另外一个方面，如果我们约去的尾数位数比较多，误差就会变得很小。

比如，如果我们约去的不是一位数而是两位数，那么从0.01到0.99一共有 99 个数想要被约为整数 0 或 1，比例就变成了49:50，这之中的误差已经非常小了。

所以在约去的小数位数较多时，四舍五入仍然具有很好的使用价值。

而我们如果需要涉及到严格的情况时，则再采用银行家舍入法即可。

后记

说是 toFixed() 使用的银行家舍入法所以表现起来不是四舍五入，但是在 Chrome 浏览器的实测中，我注意到它也并不一定都符合银行家舍入法：

(0.45).toFixed(1); // 0.5 而不是0.4
(1.45).toFixed(1); // 1.4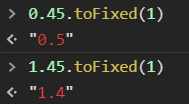

个人认为，这可能是由于浮点数存储精度问题导致的。比如这里的0.45其实类似于0.4500000002，存在一点点尾数，所以进行了舍入变为0.5。

因此，有人认为在严肃的情况下不应使用 toFixed()。所以说，如果你想要在 JavaScript 中实现四舍五入法保留两位小数，那还是乖乖 Math.round(num * 100) / 100 吧~